Apa sih Binary Search Tree itu?
Binary Search Tree atau BST adalah suatu struktur data binary tree (pohon biner) yang berbasis simpul. binary Search Tree memiliki beberapa properti, seperti :
- Subtree kiri dari suatu node hanya berisi node-node dengan kunci yang lebih rendah daripada kunci node (node key).
- Subtree kanan dari suatu node hanya berisi node-node dengan kunci yang lebih besar daripada kunci node (node key).
- Subtree kiri dan kanan masing-masing juga harus berupa sebuah Binary Search Tree.
*dengan asumsi kunci berbeda.
Binary Search Tree (BST) adalah salah satu struktur data yang mendukung pencarian yang lebih cepat, penyortiran yang cepat, dan penyisipan (insertion) dan penghapusan (deletion) yang lebih mudah. Binary Search Tree (BST) juga dikenal sebagai Sorted Version of Binary Tree.
Basic operation yang ada pada Binary Search Tree (BST), yaitu :
- Search
- Insert
- Deletion
- Pre-Order Traversal
- In-Order Traversal
- Post-Order Traversal
Yang akan kita bahas sekarang ada 3, yakni :
- Insertion
- Searching
- Deletion
Searching
Untuk mencari kunci yang diberikan (given key) di Binary Search Tree, pertama kali kita akan membandingkannya dengan akar/root. JIka kunci (key) berada di root, maka kita akan me-return root. Jika kunci (key) lebih besar daripada kunci (key) yang ada di root, kita akan melakukan pengulangan untuk Subtree kanan dari simpul root. JIkalau tidak, maka kita akan melakukan pengulangan untuk Subtree kiri.
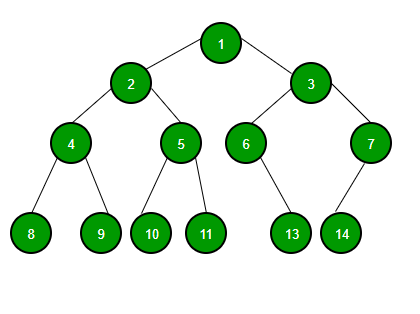
Ilustrasi untuk mencari 6 di tree di bawah ini :
- Cari di akar
- Bandingkan elemen yang di input dengan akar, jika lebih kecil daripada root, kemudian lakukan pencarian berulang pada bagian kiri atau lakukan pencarian berulang pada bagian kanan.
- Jika elemen untuk pencarian di temukan di manapun, return true, jikalau tidak, return false.

Contoh codingan :
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
Insertion
Kunci (key) baru akan selalu dimasukkan (di insert) di daun. Kita memulai untuk mencari sebuah kunci (key) dari root/akar sampai menyentuh sebuah leaf node. Sekali sebuah leaf node ditemukan, node baru akan ditambahkan sebagai anak dari leaf node.
Ilustrasi untuk menambahkan (insert) 2 di tree di bawah ini :
- Dimulai dari root
- Bandingkan elemen yang ditambahkan (di insert) dengan root/akar, jika lebih kecil dari root, maka lakukan pengulangan untuk bagian kiri. Selain itu, bisa juga melakukan pengulangan untuk bagian kanan.
- Setelah mencapai akhir, cukup masukkan simpul itu di kiri (jika kurang dari current). Jika lebih dari current, masukkan simpul di kanan.

Contoh coding untuk insertion :
/* A utility function to insert a new node with given key in BST */
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
Deletion
Ada 3 kasus yang harus di pertimbangkan :
- Jika kunci (key) berada di leaf, hapus saja node itu.
- Jika kunci (key) ada di sebuah node yang tidak memiliki chid, hapus node tersebut dan hubungkan child dengan parent nya.
- Jika kunci (key) ada di node yang memiliki 2 children (anak), temukan child yang paling kanan dari sub-tree (simpul P), ganti kuncinya dengan kunci P dan delete P secara rekursif. Atau bisa secara bergantian memilih child paling kiri dari sub-tree kanan.
Contoh coding untuk deletion :
/* Given a binary search tree and a key, this function deletes the key
and returns the new root */
struct node* deleteNode(struct node* root, int key)
{
// base case
if (root == NULL) return root;
// If the key to be deleted is smaller than the root's key,
// then it lies in left subtree
if (key < root->key)
root->left = deleteNode(root->left, key);
// If the key to be deleted is greater than the root's key,
// then it lies in right subtree
else if (key > root->key)
root->right = deleteNode(root->right, key);
// if key is same as root's key, then This is the node
// to be deleted
else
{
// node with only one child or no child
if (root->left == NULL)
{
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL)
{
struct node *temp = root->left;
free(root);
return temp;
}
// node with two children: Get the inorder successor (smallest
// in the right subtree)
struct node* temp = minValueNode(root->right);
// Copy the inorder successor's content to this node
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
Contoh Deklarasi Awal
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
Contoh Coding untuk Search Operation
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}
//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
}
return current;
}
Contoh Coding untuk Insert Operation
void insert(int data) {
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}
//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
Terima kasih :)
Referensi :
- https://www.geeksforgeeks.org/binary-search-tree-data-structure/
- https://www.tutorialspoint.com/data_structures_algorithms/binary_search_tree.html
- https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
- https://www.geeksforgeeks.org/binary-search-tree-set-2-delete/
- Slide Binus Maya